growth in spirit island
so most things in spirit island happen only once and do the same thing every time it happens. for this reason, most growths in spirit island are either constant or linear. this includes health of invaders in a land (ignoring the ramping from invader stages), or amount of cards gained over time (unless cards gained let you gain more cards). however, some things don't do the same thing every time, and therefore can cause ramping. let's look at some examples of ramping.
part 1: quadratic growths
featuring: fractured, gays, lair
so most of the non-linear growths come from doing things over and over, which is a thing that not all spirits have the ability to do.
the first things that come to mind are spirits that can do things as many times as they want, but with increasing costs for each new thing done.
this includes slip the flow of time, with an increasing time cost, and relentless punishment, with an increasing energy cost. they're both n(n-1)/2 for n uses, which is order n^2.
now for lair. if you look at the 4 moon innate on lair, it mentions a range equal to how much air lair has.
let's assume that each land has about the same size and same diameter. there are a finite number of different lands, so this can be approximately true.
so within range n of the lair would be roughly a circle of radius (n+0.5) lands. the area increases quadratically, and since the area of a land is roughly constant, the number of lands you can cover with that range increases quadratically.
part 2: n^1.5??
featuring: blight
let's say we've been adding blight to a land repeatedly. if we do the minimum cascading possible, at some point we'll have cascaded into every land within range n.
because the number of lands within range n is order n^2, and each blight added will cascade into a distinct land within range n, we'd need to add order n^2 blight to the original land to have blighted every land within range n.
because there are order n^2 lands within range n, there are order n lands at exactly range n. so to go from range n to range n+1, we have to add n times order n blight, which is order n^2 blight in total.
the sum of the first n squares is order n^3. so you're adding order n^3 blight in total to add order n^2 blight in the original land, which is a growth rate of order n^1.5.
part 3: exponential growth
featuring: lair, a second time
you've seen the air range on the 4 moon innate grows quadratically. however, more significantly, the 4 moon innate of the lair innate gathers 1 invader for every 6 explorers (and dahan) in the lair. so if there's a sufficient supply of invaders appearing near the lair, the cardinality of the lair can increase by 1/6 of its size every turn.
this is exponential growth. this is also how we managed to get 79 explorers in one land in a 3-player game.

i wonder if you can build an anti-6/6 strategy out of this.
part 4: super-exponential growth
featuring: bodan
section 4.1: intro
let's say bodan used melt earth in one land, and a town was pushed into that land.
melt earth "destroys" the town for 2 extra fear, then kicks it somewhere (or doesn't, if the isolate is used).
this essentially doubles the fear generation against towns and explorers in adjacent lands, which was used extensively with violence in one of my previous posts to generate large amounts of fear.
section 4.2: bouncing
now let's say that bodan used melt earth in two adjacent lands. now let's push a town into one of the two lands.
melt earth "destroys" the town for 2 extra fear, then kicks it into the other melt earth land, generating 2 more, for 4 in total. this triples the fear generated by towns and explorers in lands adjacent to either melted land.
this isn't super impressive, but it will increase more quickly.
section 4.3: bouncing harder
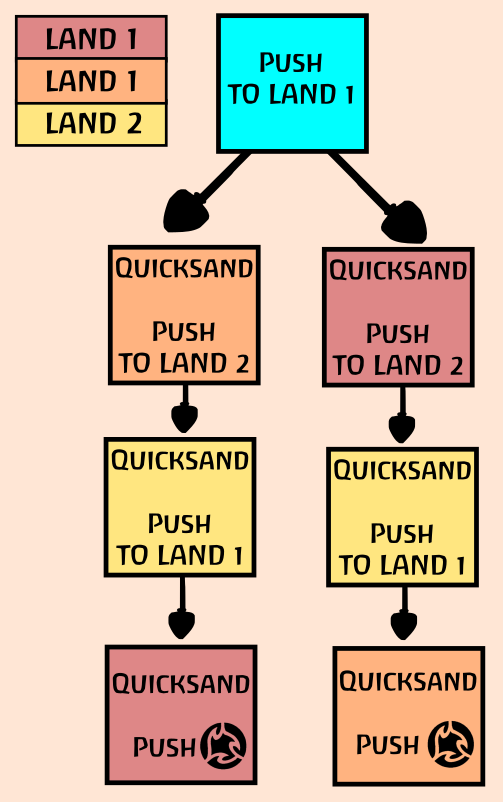
now let's say that bodan used melt earth twice in land a, and once in an adjacent land b. let's label these uses a1, a2, and b. now let's push a town into land a.
this push triggers both melt earth a1 and a2. let's resolve a1 first and kick into b, then use b kicks back into a where a2 can kick it again for 6 fear in total.
however, this is only the end of the branch that started with a1. what about the branch that started with a2?
well, if the town is still in land a when the initial a2 gets its turn to resolve, that resolution of a2 is its own branch. a2 kicks the town to b, then b kicks the town back to a, then a1 triggers again. because this is a separate branch, all 3 of these melt earths get to trigger again.
this has gone from a 3x multiplier to a 7x multiplier on fear.
this diagram made by i think mj is a pretty good explanation:
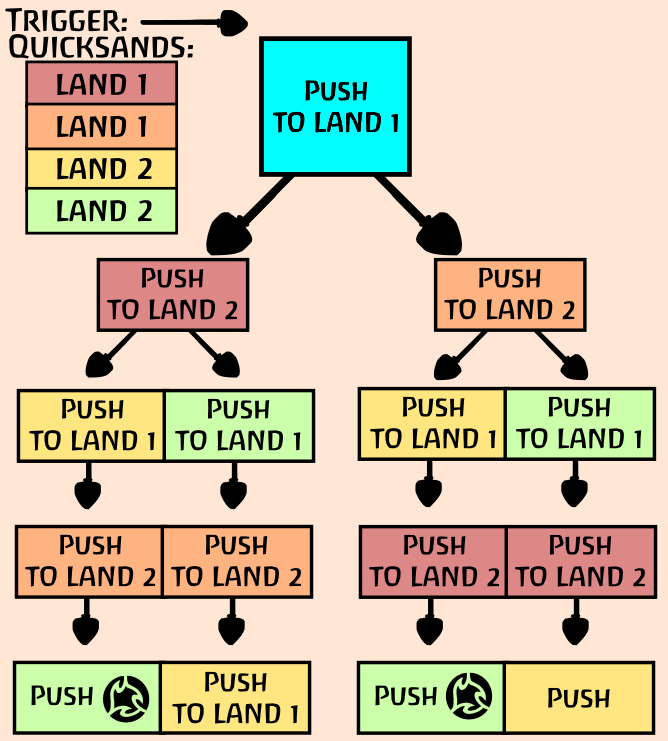
there's also this diagram for 4 uses of melt earth:
section 4.4: super-exponential growth
so let's say we have n uses of melt earth split as evenly as possible between two lands. say you push a town into the land with more uses.
it triggers ceil(n/2) melt earths, all starting their own branch. each individual branch would kick the town into the other land, which would all then start this scenario if there were n-1 uses of melt earth.
so if you define melt earth melt earth of n (shortened as meme(n)) to be the
fear multiplier of n uses of melt earth, divided as evenly as possible between
two lands.
we have meme(n)=1+ceil(n/2)*meme(n-1).
this is a factorial growth speed, which is faster than exponential.
section 4.5: what else can do this?
call to guard does approximately the same thing as melt earth, except that it doesn't automatically destroy things, but it works with badlands to destroy e.g. cowsburg towns.
also, vengeance of the dead is a similar effect that triggers every time something is destroyed in target land. it's slightly less interesting because it destroys things completely and therefore doesn't generate much fear, but it also scales factorially similarly to melt earth.
in fact, vengeance scales faster, because the number of initial triggers is n instead of ceil(n/2). however, since it's limited by amount of invader health, which doesn't grow super quickly, people haven't designed strategies around this.